I read an article the other day that really tugged at my heart. The author mourned the fact that kindergarten as it should be seems to be a thing of the past. Gone is the free play, the crayons and paint, the housekeeping center, the emphasis on learning social interactions and skills. Today there is a widespread, headlong dash towards increasing academics in kindergarten, even to the point of an increased focus on testing in kindergarten.
I’ve taught beginners both in my home and in schools. No matter how much I agree with the author’s viewpoint regarding the true work of kindergarten, I am not sure there is much we can do very soon to change the dash towards academics for beginners. What we can do is change how our children learn the basics of reading, writing, and arithmetic. If we can utilize visuals and play, kids will gain the knowledge they need, but will not feel the stress of “doing school” too early. Best of all, using visuals and play will have the effect of cutting “school time” greatly. When I taught kindergarten in my home, the children far surpassed grade level expectations, but we did all our learning through creative play and visuals, and all our learning was done in less than two hours a day including coloring and craft time. Those were the days! What we were doing was working inside a system, but not using the regular system’s methodology. What follows are some suggestions for teaching math through visuals and play.
In order to lay a solid foundation for number sense and math through play, start by using dot cards to practice seeing “how many” each number is. Doing this will allow a child to rely on her strong visual sense to understand “how many” of each number as well as to learn the combinations of numbers that equal each target number. These dot cards show various ways to arrange five dots so that not only will a child have practice just glancing and guessing “how many,” but also a strongly visual learner will begin to absorb that 5 can be made of different combinations of numbers. If you encourage your child to rely on her visual strengths, she will be much further ahead than if you sit her down to do math the old way, which is to count up, count on her fingers, or just write the answers to problems written on paper. SO BO-ring! I call the practice of learning via images, visual imprinting.
Our goal in visual imprinting activities is to connect abstract concepts to a visual image that is meaningful to your child. Visual imprinting just happens; it is a subconscious form of learning. You could call it “learning through the back door.” Visual imprinting occurs any time we see a complete picture or a specific part of a picture in our minds. Even though the idea of visual imprinting is elusive and hard to describe, we can deliberately take advantage of it in our teaching. If we can embed concepts we want a child to learn within a visual or a pattern, learning will happen unconsciously.
There are quite a few methods out there for bringing kids up to speed in computation, but the most fun and the most effortless involve visual games. Let’s create some dot cards, making the process into a craft, and then play games with the cards. If your child is having fun, he will not even know he’s learning!
Making Math Dot Cards – A Multisensory Activity
- A small stack of sturdy, square blank cards. Ideally they would be between 3½ and 4 inches on a side. Make them bigger if you’d like to.
- Tempera paint in bright colors
- Wet sponge on a plate
- Paper towels
- Old newspapers
- A place to let the cards dry
- An old shirt or smock to protect your child’s clothing
Making the Dot Cards
1. Start with one number first – say the number 3.
2. Make several dot cards using a variety of arrangements and color combinations.
3. The child will dip her fingertip into the paint and then press her fingertip carefully onto the card, making sure to only make the number of dots you planned to make.
4. The first card can have dots of the same color.
5. The second card could have one dot the same as the first card, but then the remaining two dots in a new color.
6. Name your cards according to what the pattern reminds you of. See examples below.
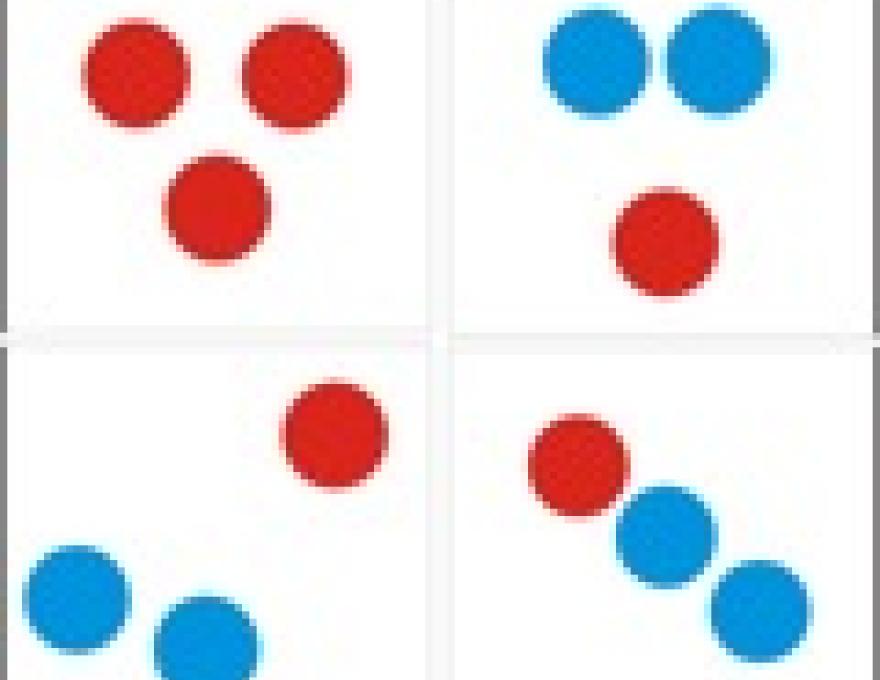
The first card just has three red dots. The second card has one red and two blue. It reminds me of a bear face. The bear has a red nose and blue eyes! In the third card, the bear is looking over his shoulder to see who is behind him. The third card can be a slide or stepping stones in the garden, or whatever else you fancy. Even if you do not stress that 3 red dots and zero other dots makes three, or that two blue dots plus one red dot make three, the child is storing up the visuals in his mind to serve as a reference point later. In addition to the visual, the child is feeling the squishy paint, smelling the tart aroma, and is seeing the color on his fingertips. It would be a powerful multisensory experience if you had your child dip three fingertips at one time in the paint because he would feel the three, see the three fingertips coated in paint, and then he’d feel and see himself transferring the color from his fingertips to the card stock.
bear has a red nose and blue eyes! In the third card, the bear is looking over his shoulder to see who is behind him. The third card can be a slide or stepping stones in the garden, or whatever else you fancy. Even if you do not stress that 3 red dots and zero other dots makes three, or that two blue dots plus one red dot make three, the child is storing up the visuals in his mind to serve as a reference point later. In addition to the visual, the child is feeling the squishy paint, smelling the tart aroma, and is seeing the color on his fingertips. It would be a powerful multisensory experience if you had your child dip three fingertips at one time in the paint because he would feel the three, see the three fingertips coated in paint, and then he’d feel and see himself transferring the color from his fingertips to the card stock.
Making More Patterns
When you make dot cards for fours, play with the arrangement of dots. The first card reminds me of a child sitting down reading a blue book. The third card looks so much like a footprint to me. The middle card could be anything. To me, it looks like sets of twins walking, as viewed by a bird flying over their heads.
Note that I have shown 3+1, 2+2, and 1+3. Use the first and last dot cards to e![]() xplore the fact that no matter how you arrange the dots, 3 dots and 1 dot will always equal four.
xplore the fact that no matter how you arrange the dots, 3 dots and 1 dot will always equal four.
One More Set
Fives are fun. Card one is a box with a blue belly button. Card two can either be a house, or a sitting bear with ![]() blue shoes. Card three could be a baby chair with pink feet. Note that in my cards, I’ve covered both combinations of numbers that equal five. Once again, two cards show the same combination of numbers (3+2 and 2+3), both equaling 5.
blue shoes. Card three could be a baby chair with pink feet. Note that in my cards, I’ve covered both combinations of numbers that equal five. Once again, two cards show the same combination of numbers (3+2 and 2+3), both equaling 5.
When you have made your dot cards through the number 10, lay them out in a safe place to dry.
Introducing the Games
Once your cards are dry and ready to use, go ahead and play some math games with them!
My own preference when using math cards with beginners (four and five year olds) was to choose dot cards that only went up to 3. The instructions were that I would toss a card on the table and the children were to quickly say how many dots. The one rule was that they were not to count the dots, but just look and guess how many. If you have more than one child playing with you, let the kids take turns answering. Go through your stack a couple of times.
The next time you meet, add cards for number 4. Talk briefly about four and the dot arrangements on the four cards, and then shuffle the cards into the stack. Play the toss game again. Add another number each day until you have all the numbers to 10 in your stack. The following games should be modeled for the children first, and then they can play independently. If you are playing with one child, no problem!
Dot Card Flash
Pair up with your child or divide your group into pairs. One child will display a card and the partner will call out how many dots he sees. Remember, no counting allowed!
War
Again, this game is played in twos. Each player has a stack of dot cards held face-down. At the signal, “1-2-3-WAR!” players lay a card down, face up, saying the number of dots on their cards. The player who played the higher number gets both cards. The object of the game is to win all the cards.
War Variation
Before players lay down their cards, each says a number aloud. When cards are played, if that number shows up in the cards played, the person who chose that number takes the cards. If neither number shows up, cards go to the center pile. The next person to correctly call a number that is played gets all the cards in the center stack. For example, player 1 calls out “7” and player 2 says “5.” Both players lay down a dot card. The cards played are 3 and 4. Since the played cards do not match the numbers called, both cards go into the center pile and new numbers are called. The next time, player 1 calls out “8” and player 2 calls out “5,” and then both players lay down a card. Cards played are 5 and 7. Player 2 gets both cards. If by chance both players call numbers that match the played cards, each player gets the card she called.
Go Fish
You will need two sets of dot cards for this game. Shuffle the stacks and deal five cards to each player. The player who goes first will look at the dot cards in his hand and will ask the second player for a card to match one he is holding. For instance, if player 1 is to go first and she has dot cards 3, 7, 1, and 9, she will ask player 2 for one of those cards. If player 2 has one, he must surrender that card to player 1 who will place the matching cards face down beside her. Player 2 then asks for a card. If the requested card is not in his partner’s hand, she will say, “go fish” and the requesting player will draw a new card from the center stack. The game ends when the one player is out of cards. The player holding the highest number of pairs wins the game.
Conclusion
Children’s brains were created beautifully – they were created to learn, but not every brain learns the same. If we will supply our children with a rich visual background for numbers, we will be allowing each brain to organize the information and store it according to how each particular brain learns and remembers best. We will be moving away from telling our children to memorize math facts, and we will be moving our children towards an understanding of numbers that will lead to success in computation. Taking this visual approach allows us to de-stress our little ones while still preparing them for future success in learning.
Sarah Major, CEO of Child1st Publications, grew up on the mission field with her four siblings, all of whom her mother homeschooled. As an adult, Sarah homeschooled a small group of children in collaboration with their parents, and has taught from preschool age to adult. Sarah was the Title 1 director & program developer for grades K-7, an ESOL teacher, and a classroom teacher. As an undergraduate student, Sarah attended Wheaton College in Wheaton, Ill. where she received a B.A. in art. Sarah then received her M.Ed. from Aquinas College in Grand Rapids, MI. In 2006 Sarah resigned from full-time teaching in order to devote more of her time to Child1st. In her spare time Sarah enjoys gardening, cooking, pottery, quilting, and spending time with her family.
Child1st Publications, LLC
704-240-9957
1379 S. Aspen St.
Lincolnton, NC 28092